一級建築士試験の構造力学計算問題について、
「何故そんな風に考えることができるのか?」
に焦点を当て、「考え方」を学ぶことで、色んな問題へ応用できるように解説します。
今回は、トラスの問題を扱います。
トラスの問題は、リッターの切断法でほとんど解けてしまいます。
ただ、どの向きで切断すればいいのかわからない、迷ってしまうということがあると思います。
例題を用いて、計算問題を解ける人がどのように考えているのか、脳内を解説します。
この記事を読めば、切断方法のコツを知ることができます!

今回の問題は3方向に切ることができます。
どんな風に考えるのか、考え方を解説します!!

問題
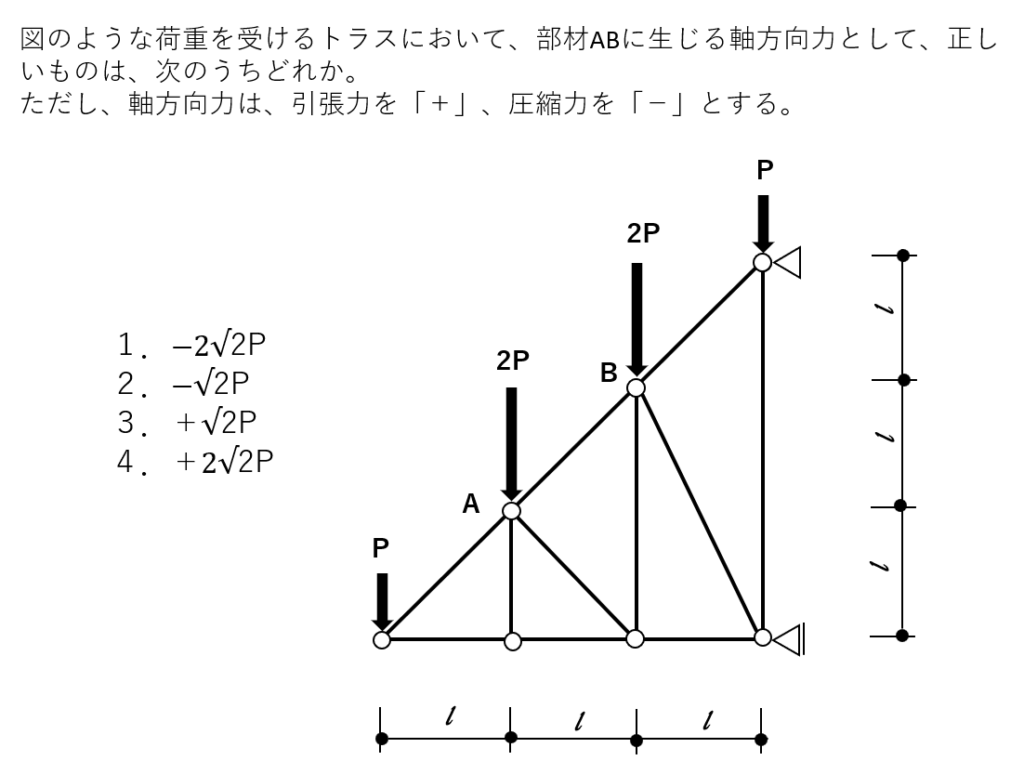
説明の流れ
今回の解説は、通常のリッターの切断法で考える流れで問題を解いた後に、
別の切断方法を考えた場合にどうなるかを考察する流れで行います。
解ける人の脳内を解説
全体方針
トラスの問題だから、リッターの切断法で解くはずだ。
リッターの切断法の大きな流れは下の4つの工程だ。
①トラスを支えている支点の反力を求める
②応力を求めたい部材を通る線でトラスを切断する
③切断したどちらか片方の部分を考える。切断面に軸方向力を仮定する
④③で選んだ部分について、力のつり合い式を立て、それを解く

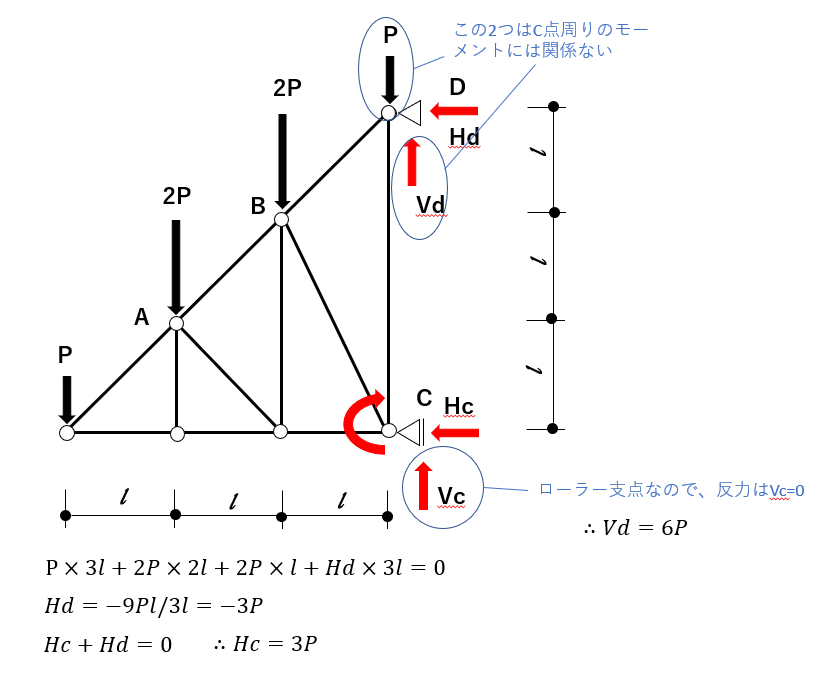
支点反力の算出
まずは、支点の反力を求めてみよう。
2つの支点でのそれぞれ反力は、下図の赤矢印の通り。
まずは、鉛直方向について、
C点をよく見るとローラー支点だから、Vc=0だ。
だから、
$Vd = P + 2P + 2P + P = 6P$
次は、水平方向について
どっちでもいいけど、今回はC点周りのモーメントのつり合いを考えてみよう。
そうすると図の下の式の通り、
$ Hd = -3P$ $Hc = 3P$
これで反力が求まった。
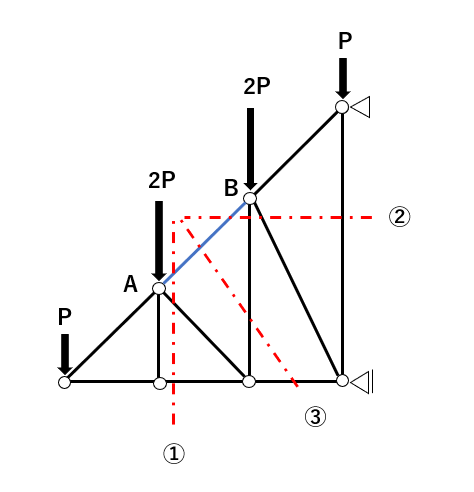
切断・軸方向力の仮定
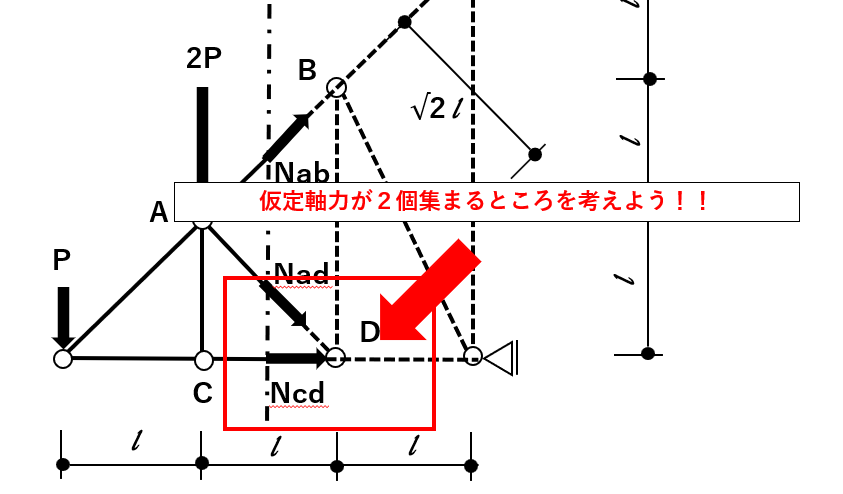
次に、応力を求めたいAB間の部材を通るように、切断面を決めて、軸方向力を仮定しよう。
今回AB間を通る切断方法は下図の①~③があるぞ。
どれが一番いいのかよくわからない。。
ひとまず、オーソドックスに①で切ってみよう。
①で切断した場合、情報量が減る方向で考えると左側を残すのが良さそうだ。
各部材の切断面で軸方向力を仮定すると下図の通り。
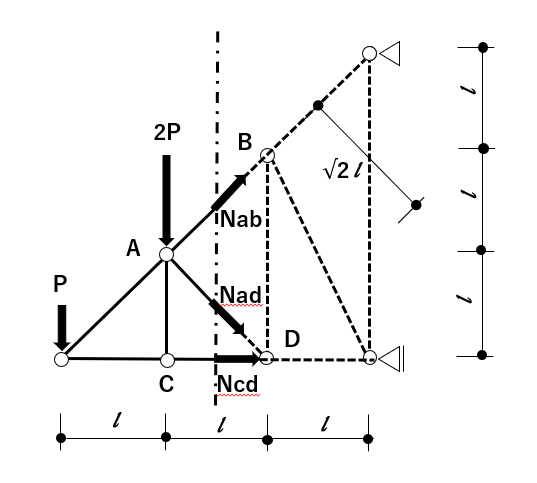
力のつり合い式を解く
選んだ部分について、力のつり合い式を立て、それを解く
ここまできたら、最後につり合い式を解くだけだ。
切断法を解く上で大事なのは、
「切断した部材も、物体は移動や回転することなく、安定している」
つまり、鉛直方向にも水平方向にも、回転方向にも、力がつり合っているということだ。
求めたい数値を確認すると、AB間の部材に作用する力だから、
今回はNabを求めればいいんだ。
Nabを求めるために、
他の自分が仮定した軸方向力(NadやNcd)は式に出てこないような、つり合い式を立てたい。
(そうしないと、連立方程式を解かないといけなくて面倒だ。)
そう考えると、今回は点D周りのモーメントを算出するのが良さそう。
切断面より左側で式を立てると
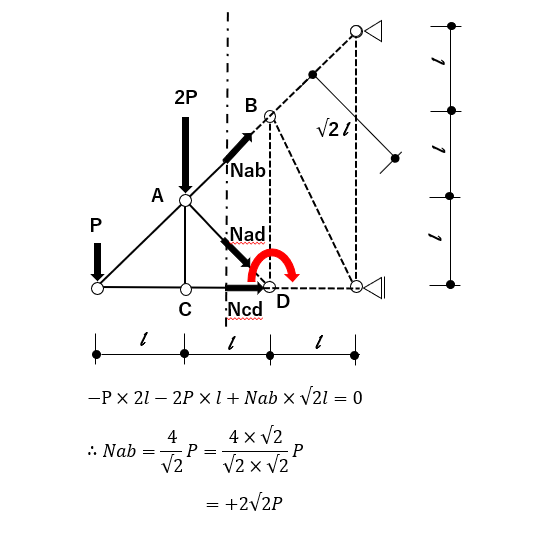
答えは④だ!

結局、反力を出したけど、使わなかった。
そこまで先を見て考える方法もあるけど、
最初はシステマティックに反力を出すことを癖にしておくと良いです。
切断方法が分からないときはどう考えるか?
さて、今回は①を選択して、すんなり問題が解けてしまった。
でも、②③でも切断できることを考えると、迷ってしまうこともあるでしょう。
そこで、実際に②や③で切った時にどうなるのか?
実際に計算をする前に考えることで、より良い切断方法が選択できるようになりましょう。
②で切断した場合
②で切った場合が下図のようになります。
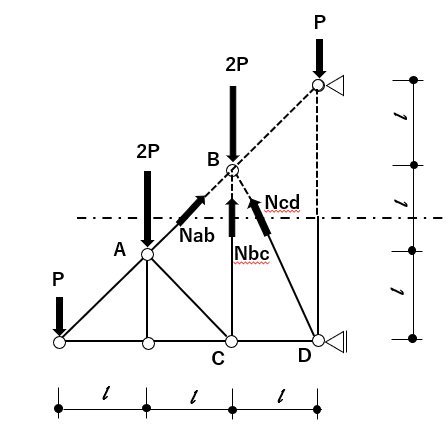
ここから、力のつり合い式を立てて、それを解くことになりますが、
それぞれの支点での力のつり合い式を立てる時どうなるか考えて見ます。
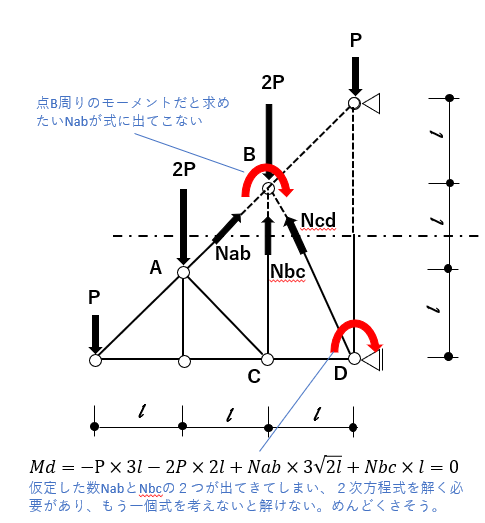
下図のように点B周りのモーメントのつり合い式では、求めたいNabが出てきません。
また、点D周りのモーメントのつり合い式では、仮定した数が2つ入ってきてしまうため、
もう一つ式を立てて、連立方程式を立てる必要が出てきて、面倒です。
③で切断した場合
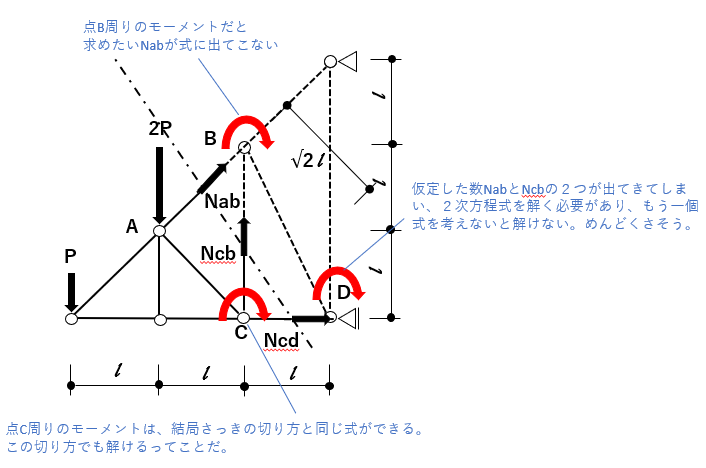
次に③で切断した場合を考えて見ます。
③で切断した場合は下図のようになります。
点Bや点D周りのモーメントのつり合い式は、②で切断した場合と同様に上手く行きませんが、
点C周りのモーメントのつり合い式は、実は①と同じ式が立てられるので、
同様に答えを求めることが出来ます。
切断方法決定のポイント
②③の例を見ていただいた通り、切断方法でモーメントのつり合い式が変わります。
そして、切断方法を決めるうえで、最初に狙うべきポイントは、
「求めたい軸方向力以外の、自分で仮定した軸方向力がつり合い式に出てこない支点があるか?」です。
今回の問題の場合、どの切断方法を考えても3つの軸方向力を仮定する必要があります。
その内の
2つが集まる点(今回の問題のD点)周りでモーメントのつり合い式が上手く立てるかがポイントになります。

最初はうまく考えられなくても、何度か練習してコツをつかんでいきましょう!!
コメント