一級建築士試験や、構造の勉強をしている中で必ず出てくるのが「振動論」です。
「論」とついた時点で、読む気がなくなりますよね。
ただ、地震が多い日本において建築を建設する場合、「振動」は避けては通れない課題です。
何故、建築士は「振動論」学ばなくてはいけないのか、実務レベルの時刻歴応答解析をわかりやすく説明しつつ、
建築士として知っておくべき振動論の基本をわかりやすく解説します。
この記事を読めば、一級建築士試験で学ぶ「振動」分野での理解が深まるとともに、免震建物や超高層建物の設計時に構造設計者がどのようなことを行いながら設計しているのかを知ることができ、打合せなどの時に適切なやり取りができるようになれます。

何故振動論を学習するのか?
さて、いきなり振動論の式を並べても読む気がなくなってしまうかと思いますので、まずは、日本の建築士が振動論を学ぶ意味を理解しましょう。
僕たちは、振動論を学んで何を知りたいのか?
難しい理論を学習するときは、数式や参考書の記述の理解するのにパワーを使い過ぎて、いつの間にか何のためにその理論を学んでいたのか忘れがちです。
そこで、まずは振動論を学んで僕たちは何を知りたいのかをはっきりさせておきましょう。
結論は、「設計する建物が地震や風などの変化する力に対して、大体どんな感じで揺れるかを調べるためです。」
結構当たり前のことのように思われるかと思いますが、「大体どんな感じ」というのが肝です。
超高層は串団子?
構造設計の作業をイメージする際、多くの方はコンピューター上に設計中の建物を再現して、その中でシミュレーションしていると考えるでしょう。
それは、その通りで、構造設計者の若者はコンピューター上に建物のモデルを構築することが最初のミッションだったりもします。(近年は、BIMから直接建物モデルに変換できるようになってきていますが。)
ただ、皆さんのイメージから少しずれるかもしれないのは、時刻歴応答解析を行う場合、その建物モデルをさらに、下の図のような串団子モデルに変換して計算を行うことが一般的です。
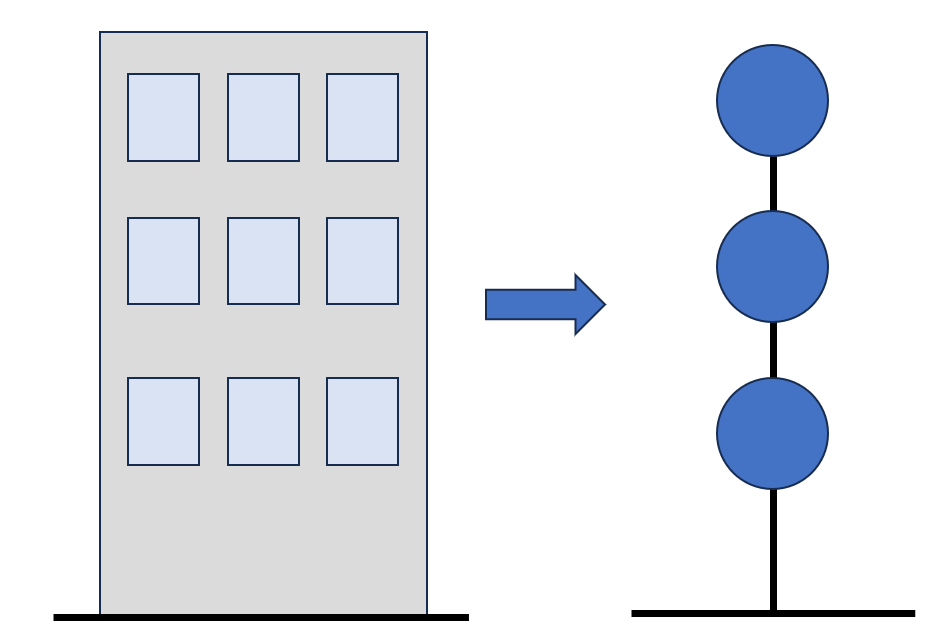
串団子の団子の部分は、その層の「質量」を表現し、串の部分は、その層の「剛性」を表現しています。
「質量」は重さなのでイメージしやすいですよね。「剛性」がイメージできない場合は、下記の記事も参照してください。

モデルが非常に単純なものになったと感じるかと思います。
何故そうするのかというと、理由は大きく2つあり、
1個目は、ひとつひとつの部材を建物の配置通りにしたモデルで振動解析を行うと、計算量が莫大で非常に時間がかかるからです。
ただ、近年は、CPU(最近はGPUか)の性能が上がっていて、その点は解消されてきており、実際にフル立体モデルで振動解析してしまうケースも多いです。
2個目は、僕たちが知りたいのは、「大体どんな感じ」で揺れるのかを知りたいだけだからです。
先ほどの、「大体どんな感じ」が出てきました。少し深堀して解説します。
何故単純なモデルで良いのか?入力地震動から考えてみる
時刻歴応答解析を行う上での、建物モデルについて、解説しました。
次に、シミュレーションに使う地震動について学びましょう。
時刻歴応答解析は、先ほどの建物モデルに対して、建物が建っている場所で地震が起こったことを再現して、計算をしています。
一般的には、6個以上の地震動を想定して、シミュレーションを行います。
この6個を多いと思うか、少ないと思うかは、個人差があるかもしれません。
ところで、あなたはこれから地震動を予測してシミュレーションを行えると思いますか?
もちろん、そんなことはできないですよね。
そうです。現代の科学においては、その場所で将来起こる地震を予測し、シミュレーションすることはできません。
なので、6個くらいの地震動を入力してみて、建物が「大体どんな感じ」で揺れるのかを確認してみるわけです。
その6個も、一応はその地盤の特性を考慮した地震動を作成するのですが、あくまでも想定でしかありません。
では、曖昧な入力に対して、建物モデルを精緻に作る意味はあるのか?ということになるわけです。
構造設計者は、想定した地震動に対して、設計中の建物が「大体どんな感じ」で揺れるのかの傾向を確認したいだけなので、建物モデルは串団子という簡易的なモデルでも十分に事足りていると考えるわけです。
ちょっと補足
上記だけを読むと凄くいい加減に設計をしているように感じますが、実際の実務では、構造設計者が重点的に知るべき内容については、個別に振動解析をしたり、静的な解析をしながら精緻な設計を行っていきます。
時刻歴応答解析を行ったうえで、地震力を低減した場合は、構造適合性判定ではなく、国土交通省大臣の認定を受ける必要が出てくるため、非常に厳しい審査が行われます。
その際も時刻歴応答解析のモデルは上記のような串団子モデルで十分審査は通ります。
上記の簡略化は、構造設計のプロ達が、工学的に合理的な方法として取り入れていると理解しておきましょう。
振動論の基礎
これまで、建築士が振動論を勉強する意義を解説してきました。
「大体どんな感じ」で揺れるのかを確認することが目的であること、時刻歴応答解析が何となく何をやっているかがわかってもらえたところで、いよいよ振動論の基礎を解説します。
覚えておきたいこと
振動とは、物体が一定の場所を中心に行ったり来たりする運動です。
例えば、振り子やギターの弦が揺れる動きが振動です。
これから学ぶ上で皆さんにイメージしてもらいたいのは、地面にばねを刺して、その上にボールを付けたようなものです。
さっき学んだ串団子のことですが、串と言いつつ、実際にはバネをイメージするとわかりやすいです。
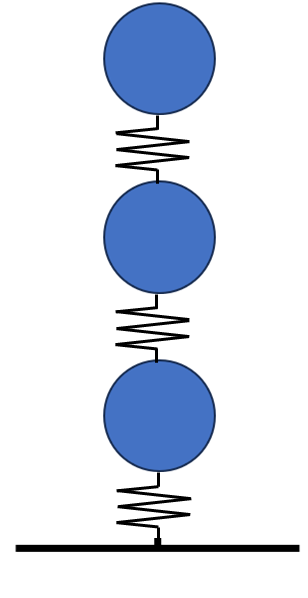
振動論は、一級建築士試験でも点がとりやすい部分です。
理由は、覚えておく公式が固有周期と水平剛性(ばね定数)の2つしかないからです。
固有周期T T = $2\pi\sqrt\frac{m}{k}$
水平剛性 K=$\frac{3EI}{L^{3}}$
固有周期って構造屋さんがたまに言っているけど、よくわからないですよね。
下記で簡単に説明します。
固有周期ってなに?
固有周期とは、その建物の揺れやすい周期(波長)のことです。
実は、建物に関わらず全ての物体は、自分が最も影響されやすい(振動しやすい)周期というものを持っています。
それは、上記の式にある通り、質量と水平剛性(水平方向に対する変形のしにくさ)で決まります。
一級建築士試験的な表現にすると
「固有周期は、質量の平方根に比例し、柱の水平剛性の平方根に反比例します。」
言葉で覚えるより、式で覚えてしまう方が簡単かもしれません。(平方根を忘れがちなので試験時は注意!)
さて、固有周期がその建物の揺れやすい周期だとすると、設計するうえでそれを知っておくのは非常に有用であることは理解できますよね。
では、実際に構造設計者がどのようにそれを活用しているのかを勉強して、
皆さんが「これ何のために勉強してんの?」ランキング上位の「応答スペクトル」について理解を深めましょう。
「これ何のために勉強してんの?」ランキング上位の「応答スペクトル」
さて、応答スペクトルを学ぶ前に、同じような名前のフーリエスペクトルについて学びましょう。
一級建築士試験では問われませんが、これを学ばないとなんで応答スペクトルを勉強するか意味不明です。
高校で物理を勉強した方は、波の合成(足し算)のような問題を解いたことがあるかもしれません。
地震動は、色々な周期の波が合成されてなりなっています。
逆を言うと、色々な周期の波に分解ができるわけです。
その色々な周期の波に分解したものには、強いものもあれば、弱いものもあります。
周期ごとの地震波の強さに分解し表したものをフーリエスペクトル(パワースペクトル)と言います。
簡単にいうと、背の順(地震の大きさ)を、固有周期の短い順に並び変えたものです。
下記に具体的な図を示します。図は縦軸が加速度、横軸が周期です。
2003年宮城県沖の地震のときの大船渡と2003年十勝沖地震の浦河のフーリエスペクトルです。
大船渡は浦河に比べて周期の短い地震波が卓越していることがわかります。
大船渡は周期が約0.5秒以下部分で振幅が大きいですが、周期が1秒以上の地震波は浦河の方が大きくなっています。
このように、地震動そのものの特性を把握するうえで、フーリエスペクトルは有用な指標となります。
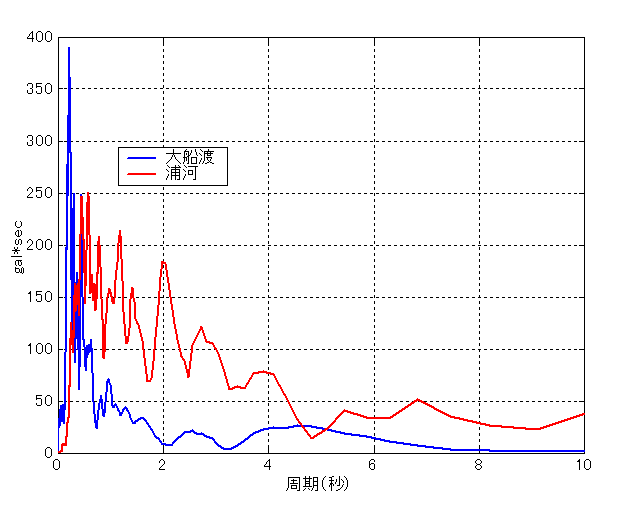
(気象庁HPより引用)
しかし、建物を設計するうえでは、その地震動を受けた建物がどのようになるか(応答するか)という方が重要です。
そこで、建物をさまざまな固有周期を持つ1質点・1自由度系に置き換え、 構造物がある地震波にさらされたときの最大応答値をスペクトルで表したものが応答スペクトルです。
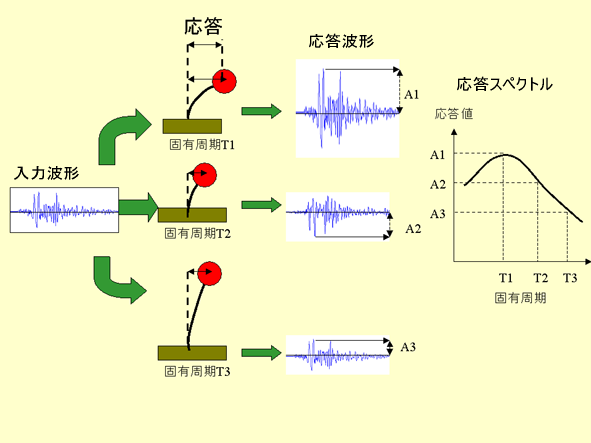
(気象庁HPより引用)
では、具体的な地震動で見てみましょう。
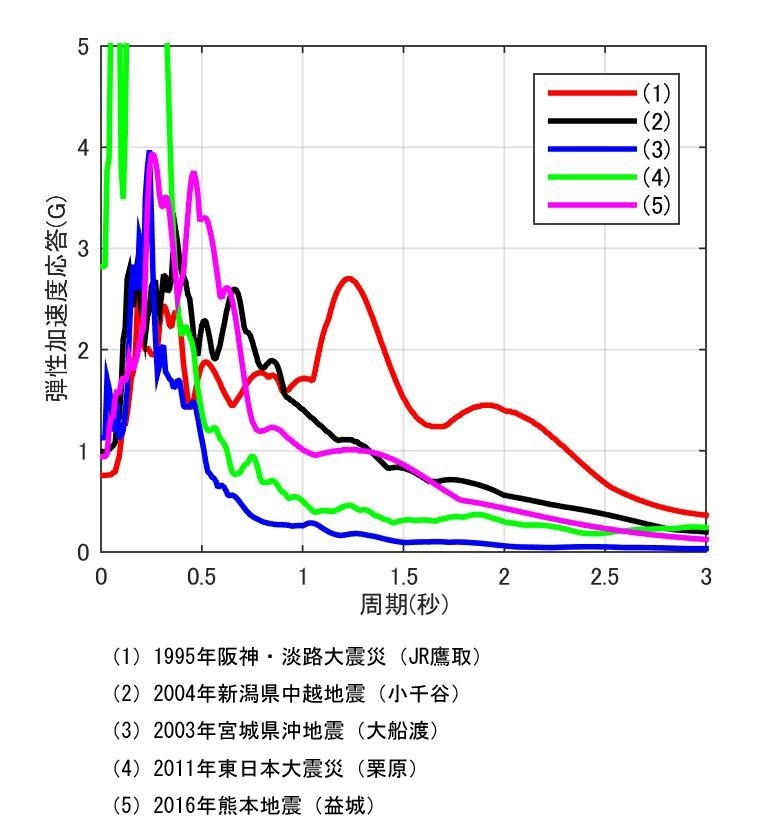
こちらは、過去日本で起きた震度7の地震動のいくつかの加速度応答スペクトル比較です。
これを見ると、どの地震動でも周期0.5秒以下部分で応答が大きく、特に東日本大震災は他の地震と比較してかなり大きいことや、阪神大震災地震は周期1.2秒前後でもう一度ピークが来ることがわかります。
応答スペクトルが大体どんなものか分かったところで、それを構造設計者が使っているかを知りましょう。
時刻歴応答解析をする時には、あるルールに則り建設地の地盤性状を反映した地震動を作成し、設計建物に入力します。(その地震動が上記に書いた6種類以上の地震動)
この地震動のパワースペクトルを描くとどの周期の地震が卓越する地盤なのかがわかります。
この地震動の応答スペクトルを描くとどの周期の建物応答が卓越するのかが把握できます。
そこに、設計中の建物の固有周期を計算で求めて、応答スペクトルに表現すると、設計中の建物に一番クリティカルな地震動が何であるかや、最大応答を大まかに把握できるわけです。
具体的に先ほどの図に落としてみましょう。今回は中層程度のビルを想定し周期2秒くらいを想定してみます。
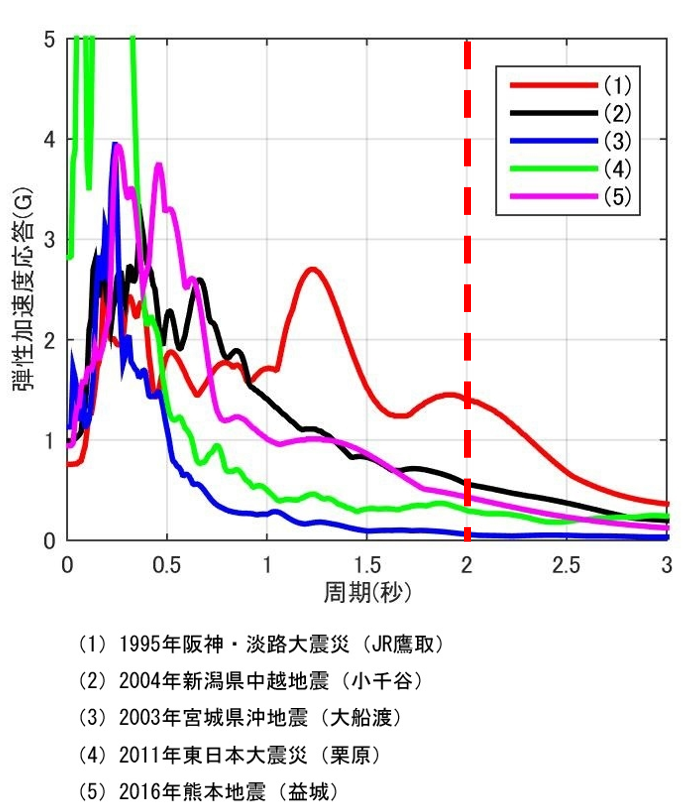
上記の図のように、周期2秒付近では、阪神淡路大震災の地震動が卓越していて、設計者としては、そちらに注意しながら設計をすることになります。
ただ、実際はこちらの図は、過去の地震動の応答スペクトルで、地盤条件などが違うので単純比較はできません。
実務では、その建設地の地盤条件を反映した地震動を作成することになり、卓越する周期も地盤の固有振動数付近にはなってきます。
上記は、「あくまで設計時に使っているイメージはこんな感じ。」くらいでとらえてください。
まとめ
振動論の重要性: 地震が頻発する日本では、建築設計において建物の揺れの応答を理解することが不可欠です。これにより、安全で耐震性の高い建物を設計できます。
振動論の目的: 地震や風などの動的な力に対する建物の揺れ方を理解し、その応答を予測するために振動論を学びます。
時刻歴応答解析: 建物モデルを用いて地震発生時の建物の揺れをシミュレーションし、その応答を分析する技術です。
串団子モデル: 建物の各層の質量と剛性を簡略化したモデルを使って、振動解析を効率的に行います。これは計算量を減らし、解析を迅速にするためです。
基本公式: 振動特性を理解するために、固有周期と水平剛性の公式を用います。固有周期は質量と剛性の平方根に依存し、建物の揺れやすさを示します。
応答スペクトル: 地震動に対する建物の応答を示すグラフで、設計において重要な指標です。建物の固有周期と地震動の特性を比較して、最大応答を予測します。

コメント