一級建築士試験の構造力学計算問題について、
「何故そんな風に考えることができるのか?」
に焦点を当て、「考え方」にフォーカスして、色んな問題へ応用できるように解説します。
今回は、トラスの問題を扱います。

トラスの問題は殆どリッターの切断法で解けるよ!
解けない場合は、他の人もできないと割り切るくらいのつもりでもいい!
トラスの問題は計算量が多いから、計算ミスしないように慎重に解こう!

問題
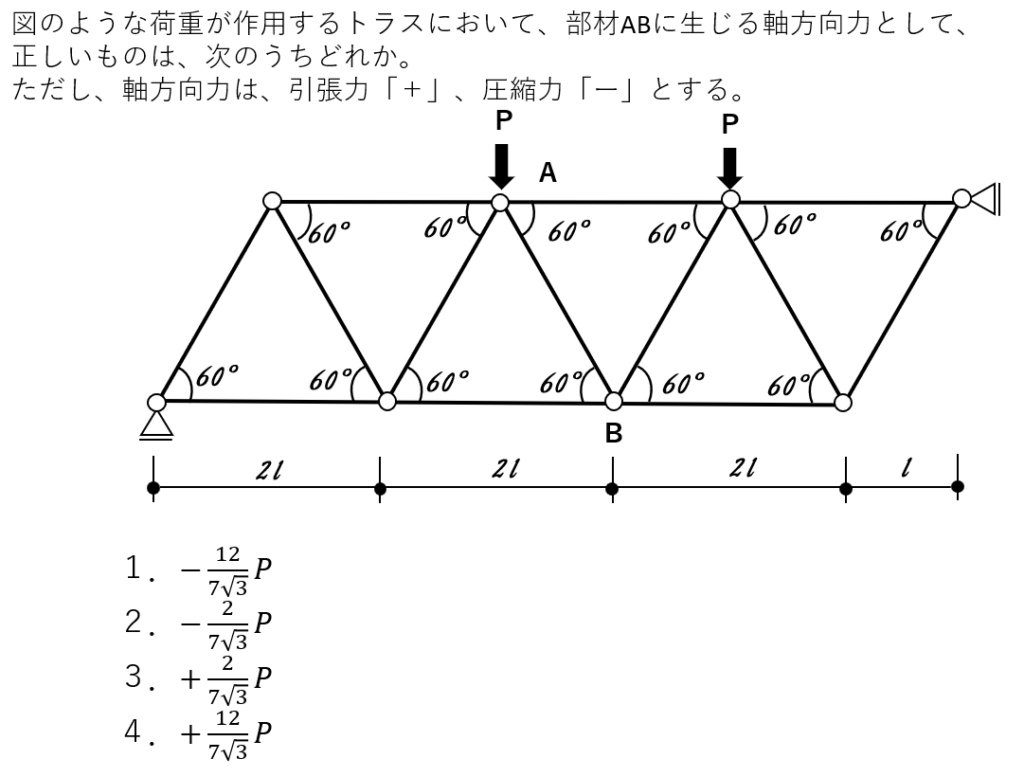
解ける人の頭の中を解説
全体方針
トラスの問題だから、リッターの切断法で解くはずだ。
リッターの切断法の大きな流れは下の4つの工程だ。
①トラスを支えている支点の反力を求める
②応力を求めたい部材を通る線でトラスを切断する
③切断したどちらか片方の部分を考える。切断面に軸方向力を仮定する
④③で選んだ部分について、力のつり合い式を立て、それを解く
支点反力の算出
まずは、支店の反力を求めてみよう。
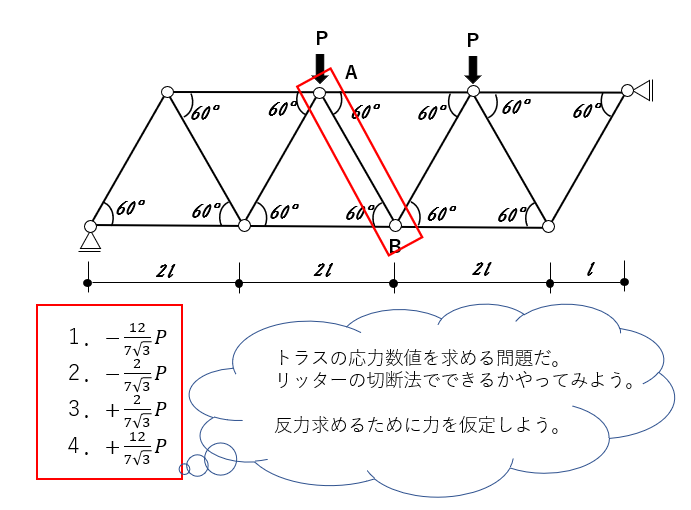
反力を求めるために、点Cか点Dのモーメントのつり合い式を考えよう。
情報量が減るのがコツだから、点Dでのモーメントのつり合い式を考えよう。
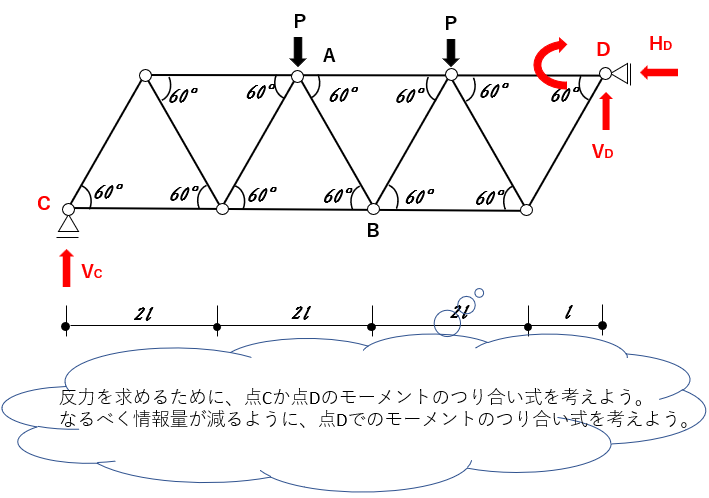
$Vc -7l -P × 4l – P × 2l = 0$
$7Vc – 6Pl = 0 $
$∴Vc =\frac{6}{7}P$
問題のトラスが上下に動いていないということは、
鉛直方向の力はつり合っているから、
$ ΣY = 0$より
$Vc-P-P+Vd=0$
$\frac{6}{7}P – P – P + Vd = 0$
$-\frac{8}{7}P +Vd= 0$
$ Vd= \frac{8}{7}P$

水平方向は、問題文でも水平に力が加わっていないから、Hdも0だよ。
部材が斜めになっているから、力が入るんじゃないかな?と思うけど、
「反力は外力と釣り合うの原則」は絶対だから間違えないように。
切断・軸方向力の仮定
これで反力が求まったから、数値を求めたい部材を通る部分で切断してみよう。
切断すると部材が2つに分かれる。
③切断したどちらか片方の部分を考える。切断面に軸方向力を仮定するだから
セオリーは情報量が少なくなる方を残すだけど、
今回はどちらも余り変わらないから左側を残すことに決めよう。
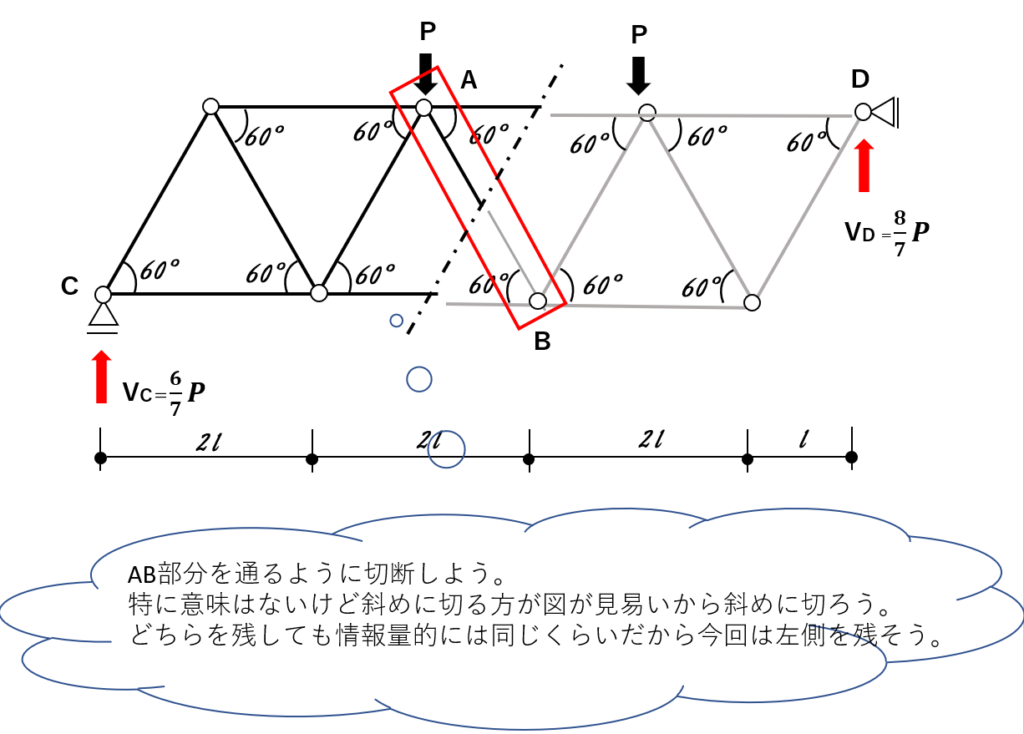
そして、切断面に軸方向力を仮定しよう
下の図の様な感じで、切断面を引っ張る方向に矢印を書いて、軸力を仮定しよう。
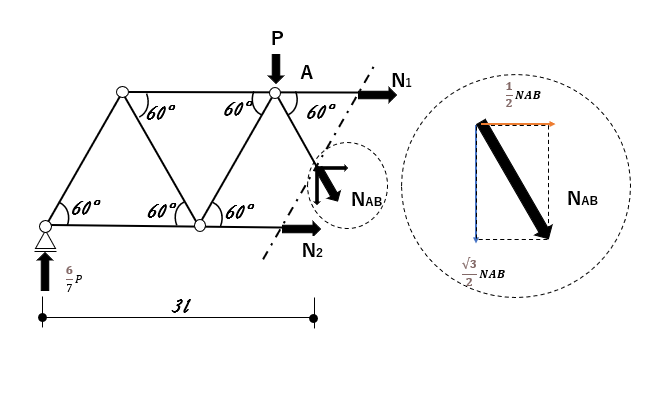
力のつり合い式を解く
選んだ部分について、力のつり合い式を立て、それを解く
ここまできたら、最後につり合い式を解くだけだ。
切断法を解く上で大事なのは、
「切断した部材も、物体は移動や回転することなく、安定している」
つまり、鉛直方向にも水平方向にも、回転方向にも、力がつり合っているということだ。
求めたい数値を確認すると、AB間の部材に作用する力だから、
今回はNABを求めればいいんだ。
NABは鉛直方向にも水平方向にも分解できるから、
どちらのつり合い式を考えても解けそうだ。
水平方向に関する情報を見ると、「N1」「N2」「√3/2NAB」で、
自分で仮定したものばっかりだから、これでは解くことができないな。
じゃあ、鉛直方向を考えてみよう。
鉛直方向もつり合っているから、
$ ΣY = 0$より
$ \frac{6}{7}P – P – \frac{\sqrt{3}}{2}Nab = 0$
$-\frac{P}{7} – \frac{3}{2}Nab = 0$
$Nab=-\frac{2}{7\sqrt{3}}P$
出来た!答えは②だ!

仮定したNabにマイナスの符号が付いたから、
仮定した「引張力」の反対の「圧縮力」だったっていうのがわかるよ。
コメント