一級建築士試験の構造分野の力学計算問題について、
「なんでそんな風に考えることができるのか?」
に焦点を当てて、「考え方」にフォーカスして、色んな問題へ応用できるように解説します。

「解ける人の頭の中」を解説していきます。
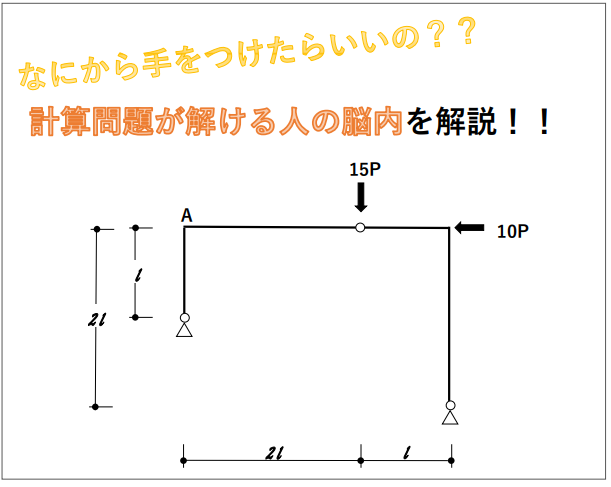
問題
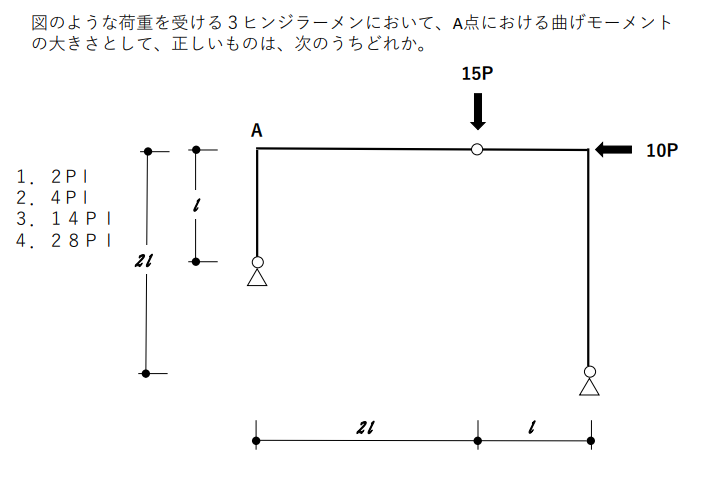
解ける人の頭の中
まず、問題をみると、A点における曲げモーメントの大きさを求める問題とわかります。
「具体的な数値を計算で出す方式ということは、方程式を解く必要があるな。じゃあ、方程式は2つくらいは必要そうだな」と考えます。
「A点周りのモーメントを求めるってことは、最後はA点周りを切り出して、力のつり合いの方程式を作って、解くってことかなー。」
「A点で切ると、左側と右側に分かれるけど、左側の方が該当部分が小さいし、情報量が少なそうだから、左側でかんがえてみるか」
「ひとまず、A点もB点も力を仮定すると下図のような感じのはず。A点のモーメントを考えると、$VB$はAB間部材と平行に作用しているから、モーメントには関係ないな。じゃあ、HBだけわかればOKだ。」
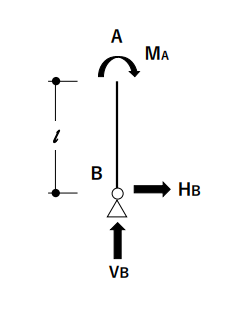
「HBを求めるために、全体の力を下図の通り全部仮定してみよう。HBを求めるためにはHBが出てくる方程式を立てて、解かないといけないから、HBが出てくるつり合い式を考えよう」
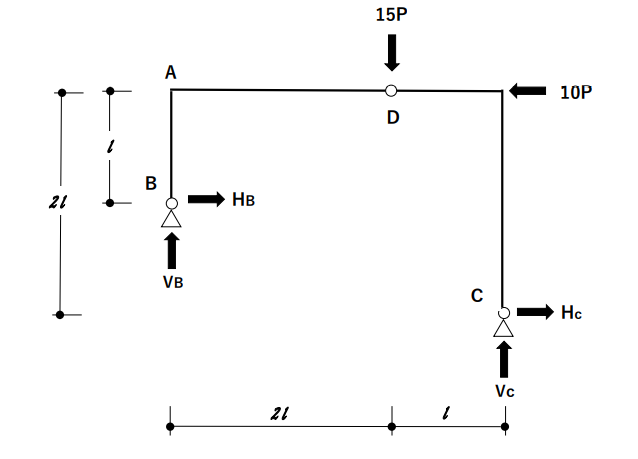
「モーメントに関するつり合いを考えてみよう。方程式立てるから、0が出てくるように考えないといけない。とすると、ピンになっていてモーメントが0になっている部分に着目しよう」
「ピンになっているのは、B、C、D点。そのうちB点周りで考えても、距離0でHBに関する情報が得られないから、C、D点について考えてみよう」
C点周りのモーメント
$VB×3l+HB×lー15P×lー10P×2l=0$
$3VBl+HBl=35Pl$・・・・・①
D点周りのモーメント
$VB×2l-HB×l=0$
$2VBlーHBl=0$・・・・・②
①と②でVBとHBの二次方程式が作れた。これを解けばVBとHBが求められるはず。
①+②から
$5VBl=35Pl ∴ VB=7P$
②に代入して解くと
$2×7P×lーHBl=0 ∴HB=14P$
求めたいと思っていたHBの値がわかった。A点で切断した図をみてA点周りのモーメントを出してみよう。この図がぐるぐる回転しないということは、A点周りのモーメントは釣り合っているということだから、HBがA点に生じさせるモーメントとMAが釣り合うはず。
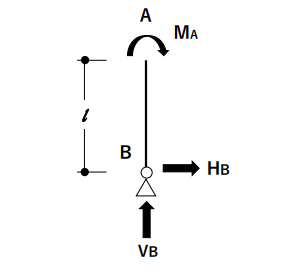
$MAーHBl=0$
$MAー14P×l=0$
$∴MA=14Pl$
出来た!答えは3!
コメント