一級建築士試験の構造分野の力学計算問題について、トラス問題は1問出題される可能性が高いです。
トラス問題は、計算量が多く、苦手に感じる人が多いかと思います。
しかし、実は、解法はパターン化されているので、それを学んで得点源にできます。
ある程度解法がわかっていれば大方の問題が解けますが、時に例外もあることを理解して、
適切な戦略で試験に臨めるようにしてきましょう。

トラス問題は、計算量が多いけど、丁寧に落ち着いて解いていけば、得点源にできるので頑張りましょう!


トラスとは
トラスとは、直線材をピン接合で接合した、三角形を基本単位として構成させる骨組みです。
荷重が節点のみに作用する場合、各部材に生じる応力(断面力)は軸力のみになります。
部材を曲げようとする力を加えないことは、非常に効率が良いです。
例えば、鉛筆を曲げようとしたら頑張れば折れそうですが、軸方向に潰すことができるか?となるとかなり難しいことはイメージできると思います。
そういったこともあり、橋や大空間等の場面で多く使われています。
一級建築士として理解をして欲しいと試験元も考えているのか、出題頻度はとても高いです。


トラスの解法の戦略
トラス問題は頻出なので、その解法を理解しましょう。
また、ある程度解法がわかっていれば大方の問題が解けますが、時に例外もあることを理解して、
適切な戦略を考えましょう。
トラスの解法には、リッターの切断法、節点法(数式)、クレモナ図解法の3つがあります。
試験問題はほとんどが、リッターの切断法で解けてしまいます。
・どんな問題を解いても同じ1点であること
・構造の試験は、時間的に余裕があり、仮に1問に時間がかかったとしても、他の問題を解く時間を失うリスクは低い
上記を考えると、
ひとまず、切断法でやってみて、解けない問題がある場合は、
潔く諦めるというのが試験対策的には有効です。
仮に切断法でトライして、問題が解けないとなっても、
合格者のみんながクレモナ図解法で鮮やかに問題解法出来る可能性が低いことを考慮すると
時間的なロスやライバルとの得点差という意味でのリスクは低いです。

リッターの切断法について
リッターの切断法は下の4つの工程で行います。
①トラスを支えている支点の反力を求める
②応力を求めたい部材を通る線でトラスを切断する
③切断したどちらか片方の部分を考える。切断面に軸方向力を仮定する
④③で選んだ部分について、力のつり合い式を立て、それを解くことで解答を得る
以上が、リッターの切断法です。
トラス以外の構造計算問題にトライしたことがある人はわかるかと思いますが、
解法の流れは、リッターの切断法も他の計算問題も同じです。
変わったことは何もしていないです。
以下に、具体例を用いて、コツも含めて解説します。
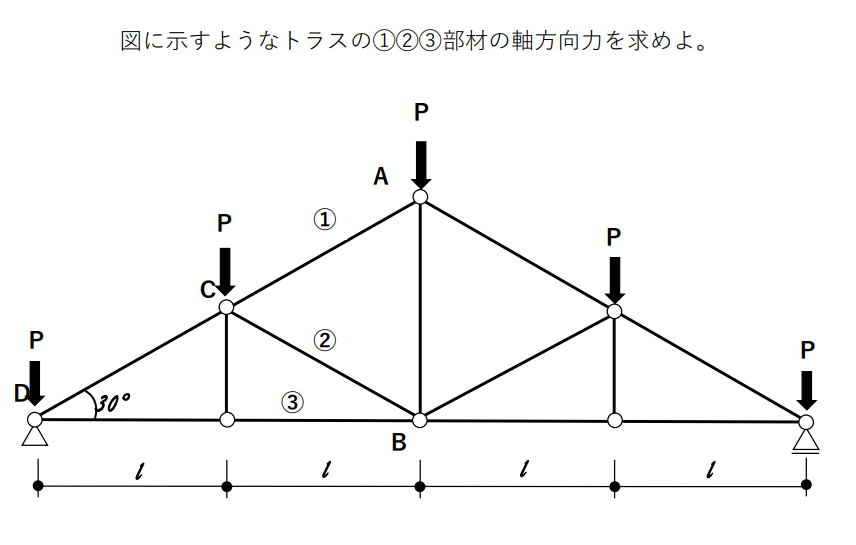
①支点の反力を求める
$5P/2=2.5P$
トラス問題の多くは、左右対称です。
左右対称の場合は、支点に作用する力は同じなので、均等にすればいいです。
もし、左右対称でない場合は、支点周りのモーメントのつり合い式を解いて反力を求めましょう。
②求めたい部材を通る線でトラスを切断する
③切断したどちらか片方の部分を考える。切断面に軸方向力を仮定する
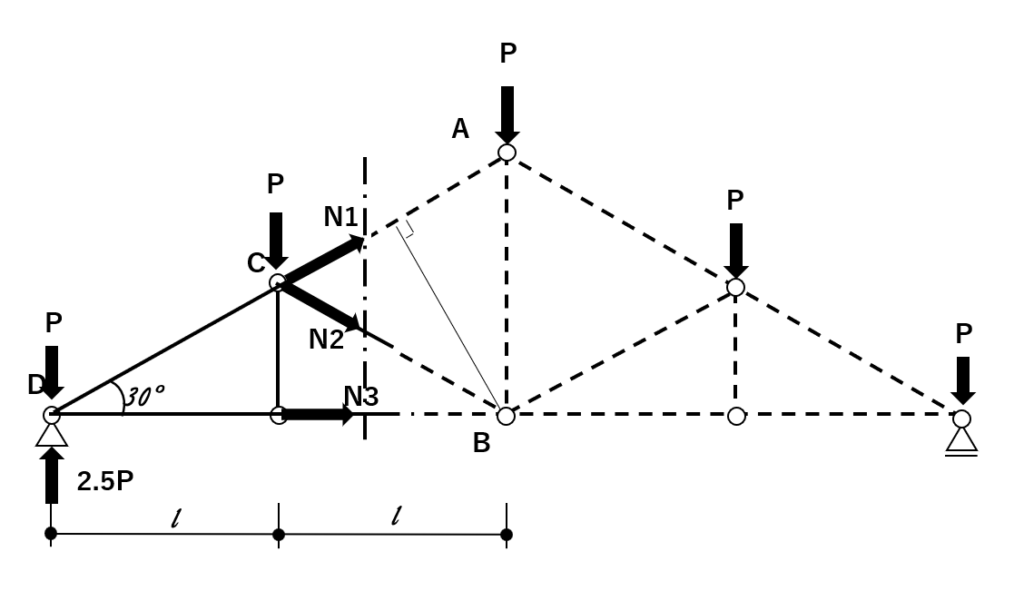
まずは、応力を求める部材を通る線でトラスを切断します。
切断した場合は、情報量が少なくなるので、小さくなる方を選ぶのが定石です。
次に、切断面で軸方向を仮定します。
仮定する力は、接点から離れる方向に矢印が向くようにしましょう。
(このようにすることで、自然と、引張が+、圧縮が-になり、符号の間違いがなくなります。)
④③で選んだ部分について、力のつり合い式を立て、それを解くことで解答を得る
<N1を求める>
力のつり合い式を立てるときのコツは、
求める応力以外の仮定した力(この場合、N2,N3)が式に出てこないようつり合い式を立てることです。
そのために、N2とN3の作用線の交点であるB点でのモーメントのつり合い式を立てます。
$ΣMB=0 2.5P × 2l – P × 2l – P × l + N1 × l = 0 $
$∴ N1=-2P $(圧縮力)
引張で仮定した力がマイナスになっているので、N1は圧縮力であることがわかります。
N2を求める場合は、D点周りのモーメントのつり合い式を立て、
N3を求める場合は、C点周りのモーメントのつり合い式を立てます。
それぞれ答えは、N2=ーP、N3=1.5√3Pです。
一度計算を解いて練習してみましょう。
コメント